上海市2025CSP-J十连测Round 5卷后感

博主： admin
发布时间：2025 年 09 月 13 日
30 次浏览
暂无评论
3887字数
分类： OI 编程

# 题目

[上海市2025CSP-J十连测Round 5](https://www.fmcraft.top/usr/uploads/2025/09/2627293367.pdf)

# 大感

难度感觉还好，我这次也是拿到了80分的成绩，试卷打印的时候少了第一道完善程序，所以这份试卷的第一道完善程序作废，不得分

# 错题大纲

## 一 单项选择

### T6

**题目：设某算法的计算时间表示为递推关系式$ T(n)=T(n-1)+n $，$ n $为正整数，$ T(0) = 1$则该算法的时间复杂度为（   ）**

> A $ O(logn) $
> B $ O(nlogn) $
> C $ O(n) $
> D $ O(n^2)$

这道题，我当时是模拟了一下，模拟的结果是这样的：

```
T(5)=T(4)+5
T(4)=T(3)+4
T(3)=T(2)+3
T(2)=T(1)+2
T(1)=0
```

此时，$n$为5，一共做了5次的$T(n)$，则时间复杂度为$O(n)$

但是错了

我估摸着是答案写错了

然后，我们邀请AI：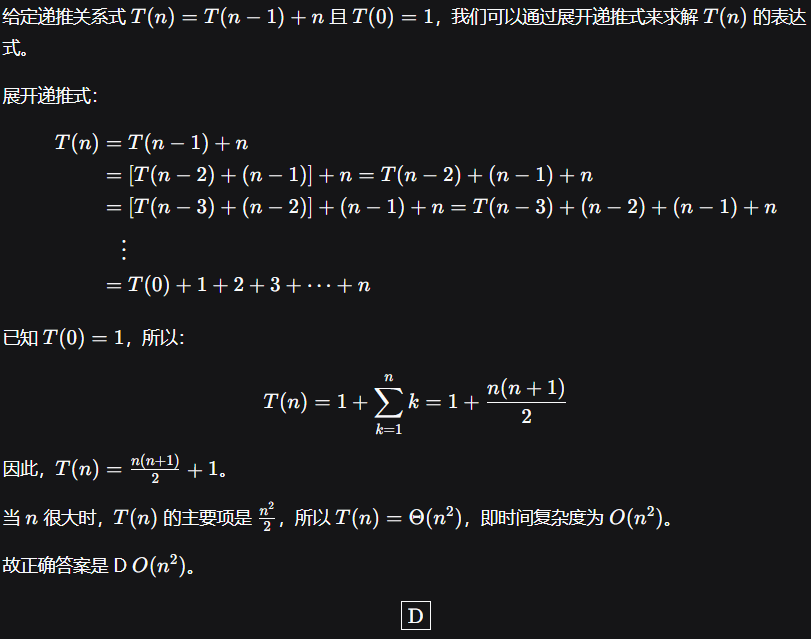

![image.png](https://www.fmcraft.top/usr/uploads/2025/09/1532168017.png)

说人话，就是模拟的数据太小了，建议增加数据模拟值

### T10

**题目：具有$n$个顶点，$e$条边的图采用邻接表存储结构，进行DFS和BFS的时间复杂度均为（   ）**

> A $O(n+e)$
> B $O(ne)$
> C $O(e^2)$
> D $O(n^2)$

我在考试中选了B，那时候我根本不知道邻接表是啥

现在让我们邀请AI

> 邻接表
> 邻接表是图的一种高效存储结构，用于表示顶点间的关联关系，尤其适合稀疏图（边数远少于顶点数平方）。
> 存储方式分两部分：
> 
> 1. **顶点表**：用数组或链表存储所有顶点信息，每个顶点元素关联一个指针，指向其邻接边的列表。
> 2. **邻接边表**：为每个顶点建立一个链表，链表节点存储与该顶点直接相连的“邻接顶点索引”及边的权重（无向图/有向图通用）。比如无向图中顶点A连B，A的邻接表含B，B的邻接表也含A；有向图中A→B仅A的邻接表含B。
>    相比邻接矩阵，邻接表节省空间，查询顶点邻接边时效率更高，是图论中常用的存储方式。

继续邀请ai分析题目

> 答案选A：$O(n+e)$
> 解析：在邻接表存储结构中，DFS（深度优先搜索）和BFS（广度优先搜索）遍历图时，每个顶点都会被访问一次（时间复杂度$O(n)$），同时每条边也会被检查一次（时间复杂度$O(e)$）。
> 两种算法的总操作次数是顶点访问次数与边检查次数的总和，因此时间复杂度均为$O(n+e)$，适用于有向图和无向图的情况。

所以，选A，说人话：分别遍历点和边

### T15

**题目：由数字1，1，2，4，8，8所组成的不同的四位数的个数是（   ）**

> A 102
> B 120
> C 560
> D 720

考试中，不知道就选C

答案为A
本题有4种情况，他们分别是**无重复数字 $A_4^4$共24种**、**含2个1（无8重复） $C_2^4 \times A_2^3=6 \times 6=36$**、**含两个8（无1重复） $C_2^4 \times A_2^3=36$**、**含两个1和两个8 C_2^4=6**，综合为102种

## 二 阅读程序

### 第一大题

```cpp
#include<iostream>
int main()
{
    int n, c;
    std::cin >> n >> c;
    long long sum = 0;
    int pre = 1000000000;
    for (int i = 0; i < n; ++i) {
        int a;
        std::cin >> a;
        if (pre > a) {
            pre = a;
        }
        sum += pre;
        pre += c;
    }
    std::cout << sum << "\n";
}
```

#### T16

**题目：当输入的a全部相等时，程序输出的结果一定等于$n \times a$**

我当时考试中填的是正确

当时也没模拟完整

考试后模拟的样例：

*input*

```
5 3
3 3 3 3 3
```

*output*

```
45
```

事实声明，本题为×

### 第二大题

```cpp
bool c[max_size][max_size] = {false};
void draw(int size, int x, int y)
{
    if (size == 1)
    {
        c[x][y] = true;
    }
    else
    {
        int half = size / 2;
        draw(half, x + half, y);
        draw(half, x, y + half);
        draw(half, x + half, y + half);
    }
}
void print(int n)
{
    int length = 1 << n;
    draw(length, 0, 0);
    for (int x = 0; x < length; ++x)
    {
        for (int y = 0; y < length; ++y)
        {
            if (c[x][y])
                std::cout << '*';
            else
                std::cout << '.';
        }
        std::cout << "\n";
    }
}
```

~~这个代码怎么不完整~~

#### T20

**题目：在`draw`的过程中，左上角的四分之一子区域始终不会被绘制**

当时我模拟是模拟到这里了

![模拟图.jpg](https://www.fmcraft.top/usr/uploads/2025/09/3006544010.jpg)

然后也懒得模拟了

如果按照这样的规律下去，那么左上角四分之一区域是会被绘制的

也不懂

估计是我题目理解问题

#### T24

**题目：`print(n)`的时间复杂度为（   ）**

> A $O(n)$
> B $O(2^n)$
> C $O(3^n)$
> D $O(4^n)$

答案为D，考试我选了B

但是deepseek的观点是选C，所以，我们需要注意：<span style='color:#FF0000'>内容由 AI 生成，请仔细甄别</span>

#### T27

**题目：程序输出的图形，是沿（   ）对称图形**

> A 对角线
> B 水平中轴
> C 垂直中轴
> D 中心镜像

考试我选择C，因为从上面那张目前模拟的地方，选C确实对于模拟没错

but

为什么错了？？？

也许是模拟错了吧

~~*其实还有另外一张模拟了一张的草稿纸，但被我当作lese扔进垃圾桶了*~~

### 第三大题

```cpp
bool valid = true;
std::vector<int> adj[max_node];
bool instack[max_node] = {false};
bool visited[max_node] = {false};
void dfs(int node)
{
    instack[node] = true;
    visited[node] = true;
    for (auto after : adj[node]) {
        if (!visited[after]) {
            visited[after] = true;
            dfs(after);
        } else if (instack[after]) {
            valid = false;
        }
    }
    instack[node] = false;
}
int main()
{
    int n, m;
    std::cin >> n >> m;
    for (int i = 0; i < m; i++)
    {
        int x, y;
        std::cin >> x >> y;
        adj[x].push_back(y);
    }
    for (int i = 1; i <= n; i++)
    {
        if (!visited[i])
        {
            dfs(i);
        }
    }
    if (valid) {
        std::cout << "Valid\n";
    } else {
        std::cout << "Invalid\n";
    }
}
```

#### T34

**题目：当输入节点数$n=10^5$，边数$m=2 \times 10^5$时，程序是否能高效运行（   ）**

> A 能，$O(n+m)$复杂度
> B 不能，$O(nm)$复杂度
> C 不能，递归栈溢出
> D 取决于图的具体结构

说实话，我考试中都不知道这个代码在干什么，全都是瞎懵的，选择题全队，选择题错了一个，即这个，考试懵了C，因为不知道就选C

让我们的deepseek来分析这道题

？？？deepseek选C？？？

*小声os：@deepseek: look in my eyes . tell me ? why ? why baby ? why ?*

## 三 完善程序

### 第一大题

S了
但是让deepseek根据题目写代码

```cpp
#include <iostream>
#include <vector>
using namespace std;

const int MAX_N = 1005;
const int MAX_M = 1005;

int main() {
    int n, N;
    cin >> n >> N;
    vector<string> P(N);
    for (int i = 0; i < N; ++i) {
        cin >> P[i];
    }
    int Q;
    cin >> Q;

// 前缀和数组，sum_black[i][j] 表示从(0,0)到(i-1,j-1)的黑格数量
    vector<vector<int>> sum_black(n + 1, vector<int>(n + 1, 0));

for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= n; ++j) {
            int pi = (i - 1) % N;
            int pj = (j - 1) % N;
            int black = (P[pi][pj] == 'B') ? 1 : 0;
            sum_black[i][j] = sum_black[i - 1][j] + sum_black[i][j - 1] - sum_black[i - 1][j - 1] + black;
        }
    }

while (Q--) {
        int A, B, C, D;
        cin >> A >> B >> C >> D;
        // 计算矩形区域内的黑格数量，注意坐标从0开始，转换为前缀和的1-based索引
        int black_count = sum_black[C + 1][D + 1] - sum_black[A][D + 1] - sum_black[C + 1][B] + sum_black[A][B];
        cout << black_count << endl;
    }

return 0;
}
```

也不知道对不对

### 第二大题

```cpp
#include<iostream>
int len(int n) {
    int length = 0;
    while (n > 0) {
        n /= 10;
        length++;
    }
    return length;
}
void print(int n, char ch) {
    while (n-- > 0) std::cout << ch;
}
int main() {
    int a, b;
    char dummy;
    std::cin >> a >> dummy >> b;
    int p = a;
    int q = b;
    while (a != 0 and b != 0) {
        if (a >= b) a %= b;
        else b %= a;
    }
    int gcd;
    if (____(1)____) gcd = b;
    else gcd = a;
    int i = p / q;
    p %= q;
    p /= gcd;
    q /= gcd;
    if (____(2)____) {
        std::cout << i << "\n";
    } else {
        int i_len = len(i);
        int p_len = len(p);
        int q_len = len(q);
        ____(3)____;
        std::cout << ____(4)____ << "\n";
        if (i != 0) std::cout << i;
        ____(5)____;
        std::cout << "\n";
        ____(6)____;
        std::cout << ____(7)____ << "\n";
    }
}
```

#### T44

考试的时候眼瞎了，看错位置了，这个是要输出杠的

# 完

致谢

最后修改：2025 年 09 月 13 日

如果觉得我的文章对你有用，请随意赞赏

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

评论 *

私密评论

名称 *

🎲

邮箱

地址

上海市2025CSP-J十连测Round 5卷后感

admin • 2025 年 09 月 13 日

# 题目

[上海市2025CSP-J十连测Round 5](https://www.fmcraft.top/usr/uploads/2025/09/2627293367.pdf)

# 大感

难度感觉还好，我这次也是拿到了80分的成绩，试卷打印的时候少了第一道完善程序，所以这份试卷的第一道完善程序作废，不得分

# 错题大纲

## 一 单项选择

### T6

**题目：设某算法的计算时间表示为递推关系式$ T(n)=T(n-1)+n $，$ n $为正整数，$ T(0) = 1$则该算法的时间复杂度为（   ）**

> A $ O(logn) $
> B $ O(nlogn) $
> C $ O(n) $
> D $ O(n^2)$

这道题，我当时是模拟了一下，模拟的结果是这样的：

```
T(5)=T(4)+5
T(4)=T(3)+4
T(3)=T(2)+3
T(2)=T(1)+2
T(1)=0
```

此时，$n$为5，一共做了5次的$T(n)$，则时间复杂度为$O(n)$

但是错了

我估摸着是答案写错了

然后，我们邀请AI：

![image.png](https://www.fmcraft.top/usr/uploads/2025/09/1532168017.png)

说人话，就是模拟的数据太小了，建议增加数据模拟值

### T10

**题目：具有$n$个顶点，$e$条边的图采用邻接表存储结构，进行DFS和BFS的时间复杂度均为（   ）**

> A $O(n+e)$
> B $O(ne)$
> C $O(e^2)$
> D $O(n^2)$

我在考试中选了B，那时候我根本不知道邻接表是啥

现在让我们邀请AI

继续邀请ai分析题目

所以，选A，说人话：分别遍历点和边

### T15

**题目：由数字1，1，2，4，8，8所组成的不同的四位数的个数是（   ）**

> A 102
> B 120
> C 560
> D 720

考试中，不知道就选C

## 二 阅读程序

### 第一大题

#### T16

**题目：当输入的a全部相等时，程序输出的结果一定等于$n \times a$**

我当时考试中填的是正确

当时也没模拟完整

考试后模拟的样例：

*input*

```
5 3
3 3 3 3 3
```

*output*

```
45
```

事实声明，本题为×

### 第二大题

~~这个代码怎么不完整~~

#### T20

**题目：在`draw`的过程中，左上角的四分之一子区域始终不会被绘制**

当时我模拟是模拟到这里了

![模拟图.jpg](https://www.fmcraft.top/usr/uploads/2025/09/3006544010.jpg)

然后也懒得模拟了

如果按照这样的规律下去，那么左上角四分之一区域是会被绘制的

也不懂

估计是我题目理解问题

#### T24

**题目：`print(n)`的时间复杂度为（   ）**

> A $O(n)$
> B $O(2^n)$
> C $O(3^n)$
> D $O(4^n)$

答案为D，考试我选了B

但是deepseek的观点是选C，所以，我们需要注意：<span style='color:#FF0000'>内容由 AI 生成，请仔细甄别</span>

#### T27

**题目：程序输出的图形，是沿（   ）对称图形**

> A 对角线
> B 水平中轴
> C 垂直中轴
> D 中心镜像

考试我选择C，因为从上面那张目前模拟的地方，选C确实对于模拟没错

but

为什么错了？？？

也许是模拟错了吧

~~*其实还有另外一张模拟了一张的草稿纸，但被我当作lese扔进垃圾桶了*~~

### 第三大题

#### T34

**题目：当输入节点数$n=10^5$，边数$m=2 \times 10^5$时，程序是否能高效运行（   ）**

> A 能，$O(n+m)$复杂度
> B 不能，$O(nm)$复杂度
> C 不能，递归栈溢出
> D 取决于图的具体结构

说实话，我考试中都不知道这个代码在干什么，全都是瞎懵的，选择题全队，选择题错了一个，即这个，考试懵了C，因为不知道就选C

让我们的deepseek来分析这道题

？？？deepseek选C？？？

*小声os：@deepseek: look in my eyes . tell me ? why ? why baby ? why ?*

## 三 完善程序

### 第一大题

S了
但是让deepseek根据题目写代码

```cpp
#include <iostream>
#include <vector>
using namespace std;

const int MAX_N = 1005;
const int MAX_M = 1005;

int main() {
    int n, N;
    cin >> n >> N;
    vector<string> P(N);
    for (int i = 0; i < N; ++i) {
        cin >> P[i];
    }
    int Q;
    cin >> Q;

// 前缀和数组，sum_black[i][j] 表示从(0,0)到(i-1,j-1)的黑格数量
    vector<vector<int>> sum_black(n + 1, vector<int>(n + 1, 0));

return 0;
}
```

也不知道对不对

### 第二大题

#### T44

考试的时候眼瞎了，看错位置了，这个是要输出杠的

# 完

致谢

上海市2025CSP-J十连测Round 5卷后感

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

IP地址修改器 [bilibili配套]

关于 2025 CSP

个人对于身高歧视的评价

FMCRAFT Res领地插件使用教程【官方 and 非官方】

关于 2025 年浙江省初中名校发展共同体七年级第一学期考试反思

【FMCRAFT 繁忙的工艺】致新玩家

【FMCRAFT 繁忙的工艺】（20251228）关于 2026 年跨年及春节期间业务安排的初步通知

教你快速搭建一个文件快递柜[filecodebox使用教程]

2023年CSP-J第一轮卷后感

上海市2025CSP-J十连测Round 6卷后感

上海市2025CSP-J十连测Round 5卷后感

发表评论 取消回复 使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

上海市2025CSP-J十连测Round 5卷后感

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款