2023年CSP-J第一轮卷后感

博主： admin
发布时间：2025 年 09 月 14 日
17 次浏览
暂无评论
2388字数
分类： OI 编程

# 试题

[2023CSP-J.pdf](https://www.fmcraft.top/usr/uploads/2025/09/333607007.pdf)

# 大感

说实话，我当时参加2023CSP-J还是五年级吧？当时只考了65分，这次再考，考了78.5分，分数线是72分（浙江）

# 错题大纲

## 一 单项选择

### T6

> 小明在某一天中依次有七个空闲时间段，他想要选出至少一个空闲时间段来练习唱歌，但他希望任意两个练习的时间段之间都有至少两个空闲的时间段让他休息。则小明一共有（   ）种选择时间段的方案
> A：31
> B：18
> C：21
> D：33

这道题，是一道经典的排列组合题
这实际上是一个组合问题，但带有约束：选取的子集中任意两个元素至少相差3
我们可以考虑用递推或组合计数的方法。这里我们采用递推（动态规划）的方法来计数所有非空子集满足约束的方案数
定义：
令 $a_n$ 表示在n个时间段中，选择至少一个时间段满足任意两个被选的时间段之间至少间隔2个（即索引差至少为3）的总方案数
注意：问题要求“至少一个”，即非空子集
实际上，我们可以先计算所有满足约束的子集（包括空集）的数量，然后减去1（空集）即可
设$f(n)$为在n个时间段中，满足任意两个被选时间段索引差至少为3的子集个数（包括空集）
考虑第n个时间段是否被选：

- 如果不选第n个，那么方案数就是前n-1个的满足约束的子集数：$f(n−1)$
- 如果选第n个，那么第n-1和n-2个都不能被选（因为要求至少间隔两个），所以前n-3个可以任意选（满足约束），因此方案数为 $f(n−3)$（注意：这里f包括空集，所以当n<3时需要小心）

因此，递推式子为：
$f(n)=f(n−1)+f(n−3)对于n≥3$
经过计算，非空为18
则答案为B

### T8

> 后缀表达式`6 2 3 + - 3 8 2 / + * 2 ^ 3 +`对应的中缀表达式为（   ）
> A `( ( 6 - ( 2 + 3 ) ) * ( 3 + 8 / 2 ) ) ^ 2 + 3`
> B `6 - 2 + 3 * 3 + 8 / 2 ^ 2 + 3`
> C `( 6 - ( 2 + 3 ) ) * ( ( 3 + 8 / 2 ) ^ 2 ) + 3`
> D `6 - ( ( 2 + 3 ) * ( 3 + 8 / 2 ) ) ^ 2 + 3`

这种题，有一种很好的方法，就是加括号，然后移符号
例如下面这个中缀表达式
`3 + 8 / 2`
先给运算加括号
`( 3 + ( 8 / 2 ) )`
然后将符号移动到当前括号的最右侧（后缀表达式）
` 3 8 2 / +`
记得删括号

所以，这道题先加括号，再转运算符后是
`6 2 3 + - 3 8 2 / + * 2 ^ 3 +`
选A

### T10

> 假设有一组字符${a,b,c,d,e,f}$，对应的频率分别为$5%,9%,12%,13%,16%,45%$。请问以下哪个选项是字符$a,b,c,d,e,f$分别对应的一组哈夫曼编码？（   ）
> A `1111 1110 101 100 110 0`
> B `1010 1001 1000 011 010 00`
> C `000 001 010 011 10 11`
> D `1010 1011 110 111 00 01`

哈夫曼编码的原理是：让频率小的字母编码长度长，频率大的字母编码长度短，因此达到文章总体编码长度更短的效果，具体过程如下，但不是题目样例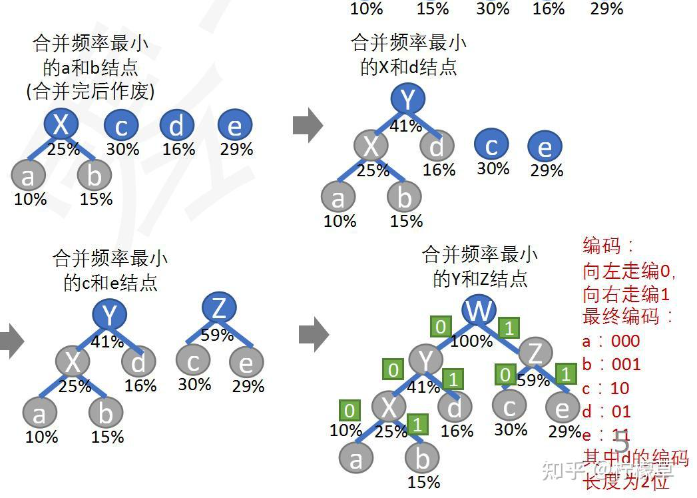
![image.png](https://www.fmcraft.top/usr/uploads/2025/09/1808376257.png)
![image.png](https://www.fmcraft.top/usr/uploads/2025/09/3284057345.png)

### T14

> 一个班级有10个男生和12个女生。如果要选出一个3人的小组，并且小组中必须至少包含一个女生，那么有多少种可能的组合？（   ）
> A 1420
> B 1770
> C 1540
> D 2200

根据题意，列出：
总共有22人（10男 + 12女），选出3人的总组合数：$C(22, 3) = \frac{22 \times 21 \times 20}{3 \times 2 \times 1} = 1540$
小组中没有任何女生（即全为男生）的组合数：$C(10, 3) = \frac{10 \times 9 \times 8}{3 \times 2 \times 1} = 120$
因此，至少包含一个女生的组合数：$\text{总组合数} - \text{全男生的组合数} = 1540 - 120 = 1420$
所以，选A

## 二 阅读程序

### 第一大题

```cpp
#include <iostream>
#include <cmath>
using namespace std;

double f(double a, double b, double c) {
    double s = (a + b + c) / 2;
    return sqrt(s * (s - a) * (s - b) * (s - c));
}

int main() {
    cout.flags(ios::fixed);
    cout.precision(4);

int a, b, c;
    cin >> a >> b >> c;
    cout << f(a, b, c) << endl;
    return 0;
}
```

### 第二大题

```cpp
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int f(string x, string y) {
    int m = x.size();
    int n = y.size();
    vector<vector<int>> v(m + 1, vector<int>(n + 1, 0));
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            if (x[i - 1] == y[j - 1]) {
                v[i][j] = v[i - 1][j - 1] + 1;
            } else {
                v[i][j] = max(v[i - 1][j], v[i][j - 1]);
            }
        }
    }
    return v[m][n];
}

bool g(string x, string y) {
    if (x.size() != y.size()) {
        return false;
    }
    return f(x + x, y) == y.size();
}

int main() {
    string x, y;
    cin >> x >> y;
    cout << g(x, y) << endl;
    return 0;
}
```

这题是LCS

### 第三大题

```cpp
#include <iostream>
#include <cmath>
using namespace std;

int solve1(int n) {
    return n * n;
}

int solve2(int n) {
    int sum = 0;
    for (int i = 1; i <= sqrt(n); i++) {
        if (n % i == 0) {
            if (n / i == i) {
                sum += i * i;
            } else {
                sum += i * i + (n / i) * (n / i);
            }
        }
    }
    return sum;
}

int main() {
    int n;
    cin >> n;
    cout << solve2(solve1(n)) << " " << solve1(solve2(n)) << endl;
    return 0;
}
```

## 三 完善程序

### 第一大题

**(寻找被移除的元素)**问题：原有长度为n+1、公差为1的等差升序数列；将数列输入到程序的数组时移除了一个元素，导致长度为n的升序数组可能不再连续，除非被移除的是第一个或最后一个元素。需要在数组不连续时，找出被移除的元素
试补全程序

```cpp
#include <iostream>
#include <vector>

using namespace std;

int find_missing(vector<int>& nums) {
    int left = 0, right = nums.size() - 1;
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == mid + ①) {
            ②
        } else {
            ③
        }
    }
    return ④;
}

int main() {
    int n;
    cin >> n;
    vector<int> nums(n);
    for(int i = 0; i < n; i++)cin >> nums[i];
    int missing_number = find_missing(nums);
    if (missing_number == ⑤) {
        cout << "Sequence is consecutive" << endl;
    } else {
        cout << "Missing number is " << missing_number << endl;
    }
    return 0;
}
```

#### T33

选B，
为什么不选A？
因为题目说了，**除非被移除的是第一个或最后一个元素**，则代表**输入的第一个数可能不是1**，所以需要用`num[0]`

#### T35

选C，自行模拟

### 第二大题

**(编辑距离)**给定两个字符串，每次操作可以选择删除Delete、 插入insert、替换Replace个字符，求将第一个字符串转换为第二个字符串所需要的最少操作次数

试 补 全 动 态 规 划 算 法

```cpp
#include <iostream>
#include <string>
#include <vector>
using namespace std;

int min(int x, int y, int z) {
    return min(min(x, y), z);
}

int edit_dist_dp(string str1, string str2) {
    int m = str1.length();
    int n = str2.length();
    vector<vector<int>> dp(m + 1, vector<int>(n + 1));

for (int i = 0; i <= m; i++) {
        for (int j = 0; j <= n; j++) {
            if (i == 0)
                dp[i][j] = ①;
            else if (j == 0)
                dp[i][j] = ②;
            else if (③)
                dp[i][j] = ④;
            else
                dp[i][j] = 1 + min(dp[i][j - 1], dp[i - 1][j], ⑤);
        }
    }
    return dp[m][n];
}

int main() {
    string str1, str2;
    cin >> str1 >> str2;
    cout << "Mininum number of operation:"
         << edit_dist_dp(str1, str2) << endl;
    return 0;
}
```

#### T40

选A
![image.png](https://www.fmcraft.top/usr/uploads/2025/09/2357809956.png)

# 完

致谢

最后修改：2025 年 09 月 14 日

如果觉得我的文章对你有用，请随意赞赏

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

评论 *

私密评论

名称 *

🎲

邮箱

地址

2023年CSP-J第一轮卷后感

admin • 2025 年 09 月 14 日

# 试题

[2023CSP-J.pdf](https://www.fmcraft.top/usr/uploads/2025/09/333607007.pdf)

# 大感

说实话，我当时参加2023CSP-J还是五年级吧？当时只考了65分，这次再考，考了78.5分，分数线是72分（浙江）

# 错题大纲

## 一 单项选择

### T6

因此，递推式子为：
$f(n)=f(n−1)+f(n−3)对于n≥3$
经过计算，非空为18
则答案为B

### T8

所以，这道题先加括号，再转运算符后是
`6 2 3 + - 3 8 2 / + * 2 ^ 3 +`
选A

### T10

### T14

## 二 阅读程序

### 第一大题

```cpp
#include <iostream>
#include <cmath>
using namespace std;

double f(double a, double b, double c) {
    double s = (a + b + c) / 2;
    return sqrt(s * (s - a) * (s - b) * (s - c));
}

int main() {
    cout.flags(ios::fixed);
    cout.precision(4);

int a, b, c;
    cin >> a >> b >> c;
    cout << f(a, b, c) << endl;
    return 0;
}
```

### 第二大题

```cpp
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

bool g(string x, string y) {
    if (x.size() != y.size()) {
        return false;
    }
    return f(x + x, y) == y.size();
}

int main() {
    string x, y;
    cin >> x >> y;
    cout << g(x, y) << endl;
    return 0;
}
```

这题是LCS

### 第三大题

```cpp
#include <iostream>
#include <cmath>
using namespace std;

int solve1(int n) {
    return n * n;
}

int main() {
    int n;
    cin >> n;
    cout << solve2(solve1(n)) << " " << solve1(solve2(n)) << endl;
    return 0;
}
```

## 三 完善程序

### 第一大题

```cpp
#include <iostream>
#include <vector>

using namespace std;

#### T33

选B，
为什么不选A？
因为题目说了，**除非被移除的是第一个或最后一个元素**，则代表**输入的第一个数可能不是1**，所以需要用`num[0]`

#### T35

选C，自行模拟

### 第二大题

试 补 全 动 态 规 划 算 法

```cpp
#include <iostream>
#include <string>
#include <vector>
using namespace std;

int min(int x, int y, int z) {
    return min(min(x, y), z);
}

int edit_dist_dp(string str1, string str2) {
    int m = str1.length();
    int n = str2.length();
    vector<vector<int>> dp(m + 1, vector<int>(n + 1));

int main() {
    string str1, str2;
    cin >> str1 >> str2;
    cout << "Mininum number of operation:"
         << edit_dist_dp(str1, str2) << endl;
    return 0;
}
```

#### T40

选A
![image.png](https://www.fmcraft.top/usr/uploads/2025/09/2357809956.png)

# 完

致谢

2023年CSP-J第一轮卷后感

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

IP地址修改器 [bilibili配套]

关于 2025 CSP

个人对于身高歧视的评价

FMCRAFT Res领地插件使用教程【官方 and 非官方】

关于 2025 年浙江省初中名校发展共同体七年级第一学期考试反思

【abc436】AtCoder Beginner Contest 436

个人对于身高歧视的评价

梦熊周赛【MX-J26 MX-X23 月亮赛】卷后感

乙巳岁九月十四修博客服务器感怀

上海市2025CSP-J十连测Round 7卷后感（Part 1）

2023年CSP-J第一轮卷后感

发表评论 取消回复 使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

2023年CSP-J第一轮 卷后感

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

2023年CSP-J第一轮卷后感